sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

setembro 20, 2021

 sistema indeterminístico Graceli ;

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

 SISTEMA GRACELI INFINITO-DIMENSIONAL.

COM  ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.

ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.

  TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA.

SISTEMA MULTIDIMENSIONAL  GRACELI

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].

DENTRO DE UMA CONCEPÇÃO QUE CADA ÁTOMO É FORMADO DE INFINITAs OUTRAS PARTÍCULAS, E COM INFINITAS OUTRAS ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, E OUTROS FENÔMENOS, LOGO SE TEM EM CADA ÁTOMO E OU ELEMENTO QUÍMICO INFINITAS OUTRAS DIMENSÕES. COM INFINITAS VARIAÇÕES NAS CATEGORIAS DE GRACELI , QUE  SÃO: OS POTENCIAIS, TIPOS, NÍVEIS, E TEMPO DE AÇÃO ESPECÍFICO  DO FENÔMENO.

ONDE NOS SISTEMAS  DE GRACELI CATEGORIAS,  FENÔMENOS, ESTADOS, ENERGIAS, ESTRUTURAS, E OUTROS SÃO TIPOS E FORMAS DE DIMENSÕES..

FLUXOS ALEATÓRIOS DE ENERGIAS ELÉTRICA,  E FLUXOS DE SALTOS QUÂNTICOS INFINITESIMAIS E INDETERMINADOS.

SENDO QUE VARIAM CONFORME O SISTEMA INFINITO-DIMENSIONAL GRACELI.

Fórmula de Landau-Zener

Origem: Wikipédia, a enciclopédia livre.

Cruzamento evitado mostrando o perfil dos valores próprios de um hamiltoniano de um sistema de dois níveis em função de uma coordenada z. Os valores próprios (energia dos estados adiabáticos) seguem um perfil hiperbólico, em que a energia dos estados diabáticos são assímptotas com uma evolução linear em z.

A fórmula de Landau–Zener é uma expressão matemática para a probabilidade de transição entre dois níveis de energia numa situação de cruzamento evitado. Corresponde a uma solução analítica das equações de movimento que regem a dinâmica de um sistema mecânico quântico de 2-níveis de energia, com um hamiltoniano dependente do tempo variando de tal forma que a separação de energia dos dois estados (diabáticos) é uma função linear do tempo, e o acoplamento entre esses dois estados é constante. A fórmula foi publicada separadamente por Lev Landau,^[1] Clarence Zener,^[2] Ernst Stueckelberg,^[3] and Ettore Majorana,^[4] em 1932.

• 5Ver também

Fórmula de Landau-Zener

A fórmula de Landau-Zener tem tido um papel central na descrição de efeitos não-adiabáticos (envolvendo mais do que um estado electrónico) em colisões atómicas e moleculares ^[5] em particular, e efeitos não-adiabáticos na química e física molecular em geral.^[6] Neste contexto, considera-se que o sistema se move com uma velocidade constante v e que a variação ao longo da coordenada z dos níveis de energia do sistema é uma hipérbole. A probabilidade de um sistema que começa num dos níveis de energia terminar no outro nível de energia depois de atravessar o centro da hipérbole em z_c, em que o intervalo que separa os dois níveis de energia é menor, é dada pela fórmula de Landau-Zener

${\displaystyle p_{LZ}=exp\left(-{\frac {\pi ^{2}\Delta V^{2}}{h\Delta Fv}}\right)}$,

///////////////////////////////////////////////////////////////

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

em que ΔV é a diferença energética dos dois níveis no ponto z_c, ΔF é a diferença do declive das assimptotas da hipérbole e h é a constante de Planck.

A fórmula de Landau-Zener fornece resultados razoáveis quando a energia cinética do sistema é elevada, mas sobretudo é um modelo paradigmático para racionalizar efeitos não-adiabáticos.^[7]

Fórmula de Stueckelberg

Numa colisão atómica ou molecular os sistema atravessa a região de interacção duas vezes.

Numa colisão atómica ou molecular, o sistema atravessa por duas vezes a região z_c em que a energia dos dois níveis se aproxima. A probabilidade de um sistema que se encontra num determinado nível de energia antes da colisão e terminar num outro após a colisão, foi determinada por Stueckelberg ^[3]

${\displaystyle p_{S}=4p_{LZ}(1-p_{LZ})\sin ^{2}(\Phi +\varphi )}$,

///////////////////////////////////////////////////////////////

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

em que p_LZ é a probabilidade de transição numa passagem dada pela fórmula da Landau-Zener, Φ é a diferença de fases acumulada pela função de onda do sistema entre as duas passagens por z_c, e φ é uma fase dinâmica que tende para φ=π/4 no limite de velocidades elevadas.^[7]

Notas

Sistema adiabático

Origem: Wikipédia, a enciclopédia livre.

(Redirecionado de Adiabático)

Um sistema adiabático (em grego: ἀδιάβατος; romaniz.: adiabatos , "impenetrável")^[1] é, na física, um sistema que está isolado de quaisquer trocas de calor.

É uma qualidade relativa à fronteira que delimita e determina o que vem a ser um sistema físico e por conseguinte o que se chama de sua vizinhança. Uma fronteira adiabática isola completamente o sistema de sua vizinhança no que tange a troca de matéria ou ao calor.

Na termodinâmica, associa-se também a processos ou transformações^[2] que ocorrem no interior de fronteiras adiabáticas, havendo ausência de troca de energia na forma de calor com a vizinhança. Geralmente é aceito, entretanto, que uma fronteira adiabática não é completamente restritiva em relação à troca de energia, havendo a "flexibilidade" de que o volume encerrado pela fronteira se altere em processos ditos adiabáticos, o que por conseguinte pode levar à troca de energia entre o sistema e sua vizinhança na forma de trabalho.

Observa-se experimentalmente que processos que ocorram muito rapidamente em sistemas fechados podem ser tratados como processos adiabáticos, mesmo que as fronteiras que definam os respectivos sistemas não o sejam. Isto ocorre porque não há tempo para trocas de calor significativas entre o meio e sua vizinhança.^[3] Como exemplos têm-se a compressão súbita do ar em uma seringa e um fenômeno climático que ocorre na atmosfera terrestre no qual uma parcela de ar aquecido, forçada a subir por convecção, se expande devido à diminuição da pressão atmosférica com a altitude, e se esfria devido a esta expansão (resfriamento adiabático e Vento Foehn). Inversamente, processos muito lentos, em que a temperatura do sistema permanece constante pela troca de calor com o ambiente, podem ser tratados como processos isotérmicos.

Um processo adiabático pode ser descrito pela expressão ${\displaystyle \delta Q=0}$ onde ${\displaystyle \delta Q}$ é a energia transferida pelo aquecimento (ou resfriamento). Pela segunda lei da termodinâmica, ${\displaystyle \delta Q=TdS}$ para um processo reversível (onde T é a temperatura e S é a entropia), um processo adiabático reversível é também um processo isentrópico (${\displaystyle dS=0}$). Entretanto, para um processo irreversível, ${\displaystyle \delta Q<TdS}$ de modo que um processo adiabático irreversível não é isentrópico.

Um extremo oposto — permite transferência de calor com ambiente, fazendo com que a temperatura permaneça constante — é conhecido como um processo isotérmico. Como a temperatura é termodinamicamente conjugada à entropia, o processo isotérmico é conjugado ao processo isentrópico, e portanto a um processo adiabático reversível.

Uma curva adiabática é a representação, em um gráfico adequadamente dimensionado, da relação existente entre os valores de grandezas como pressão, volume e temperatura assumidos para o sistema que, sofrendo transformações, vai de um estado inicial P1, V1 e T1 para um estado final P2, V2 e T2, mantidas as condições de que não haja troca de calor ou matéria com o meio circunvizinho na passagem de um estado ao outro.

• 6Ligações externas

Gás ideal (processo reversível)

Para uma substância simples, durante um processo adiabático no qual o volume aumenta, a energia interna da substância que realiza trabalho deve diminuir.

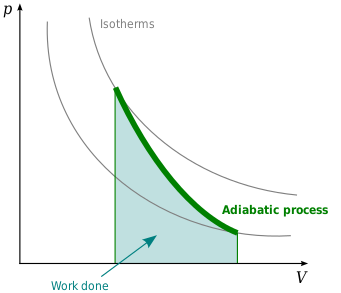
A equação matemática para um gás ideal passando por um processo adiabático reversível é

${\displaystyle PV^{\gamma }=\operatorname {constante} \qquad }$

onde P é a pressão, V é o volume, e

${\displaystyle \gamma ={C_{P} \over C_{V}}={\frac {f+2}{f}}}$

///////////////////////////////////////////////////////////////

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

${\displaystyle C_{P}}$ sendo o calor específico para pressão constante, ${\displaystyle C_{V}}$ sendo o calor específico para volume constante, ${\displaystyle \gamma }$ é o coeficiente de expansão adiabática, e ${\displaystyle f}$ é o número de graus de liberdade (3 para um gás monoatômico, 5 para um gás diatômico e moléculas colineares).

Para um gás ideal monoatômico, ${\displaystyle \gamma =5/3\,}$, e para um gás diatômico (como nitrogênio e oxigênio, principais componentes do ar) ${\displaystyle \gamma =7/5\,}$.^[4] Note que a fórmula acima se aplica somente a gases ideais clássicos e não Bose–Einstein ou Fermi gases.

Para processos adiabáticos reversíveis, também é correto afirmar que

${\displaystyle P^{1-\gamma }T^{\gamma }=\operatorname {constante} }$

${\displaystyle VT^{f/2}=\operatorname {constante} }$

onde T é uma temperatura absoluta.

Isto também pode ser escrito como

${\displaystyle TV^{\gamma -1}=\operatorname {constante} }$

Exemplo de compressão adiabática

Vejamos agora um exemplo comum de compressão adiabática, - a compressão em um cilindro de um motor de combustão interna. Faremos algumas suposições simples: que o volume descompactado do cilindro é 1000 cm³ (um litro), que o gás em seu interior é quase que puramente nitrogênio (portanto um gás diatômico com cinco graus de liberdade e assim ${\displaystyle \gamma }$ = 7/5), e a taxa de compressão do motor é 10:1 (isto é, o volume de 1000 cm³ de gás descompactado irá comprimir-se até 100 cm³ quando o pistão for de baixo para cima). O gás descompactado está aproximadamente a temperatura e pressão ambientes (temperatura de 27 °C, e pressão de 1 atm ~ 100000 Pa).

${\displaystyle PV^{\gamma }=\operatorname {constante} =100.000\operatorname {Pa} \cdot 1000^{7/5}=100\times 10^{3}\cdot 15,8\times 10^{3}=1,58\times 10^{9}}$

então nossa constante adiabática para esse experimento é aproximadamente 1.58 bilhões.

O gás é agora compactado até um volume de 100 cm³ (iremos supor que isso ocorre suficientemente rápido para que nenhum calor penetre ou deixe o gás). O novo volume é 100 cm³, mas a constante para esse experimento ainda é 1.58 bilhões:

${\displaystyle PV^{\gamma }=\operatorname {constante} =1,58\times 10^{9}=P\cdot 100^{7/5}}$

resolvendo para P:

${\displaystyle P=1,58\times 10^{9}/{100^{7/5}}=1,58\times 10^{9}/630,9=2,50\times 10^{6}\operatorname {Pa} }$

ou em torno de 24.5 atm. Note que esse aumento da pressão é mais do que uma simples taxa de compressão de 10:1 indicaria; isso porque o gás não é somente compactado, mas o trabalho exercido para comprimir o gás também o aquece, e quanto mais quente o gás maior a pressão, mesmo que o volume não tenha mudado.

Podemos resolver para a temperatura do gás compactado no cilindro do motor também, usando a lei dos gases ideais. Nossas condições iniciais são 100000 Pa para pressão, 1000 cm³ de volume, e 300 K para temperatura, então nossa constante experimental é:

${\displaystyle {PV \over T}=\operatorname {constante} ={{10^{5}\cdot 10^{3}} \over {300}}=3,33\times 10^{5}}$

///////////////////////////////////////////////////////////////

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

Sabemos que o gás compactado possui um V = 100 cm³ e P = 2.5E6 pa, então podemos resolver para a temperatura por simples álgebra:

${\displaystyle {PV \over {\operatorname {constante} }}=T={{2,50\times 10^{6}\cdot 100} \over {3,33\times 10^{5}}}=751}$

///////////////////////////////////////////////////////////////

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

Essa é uma temperatura final de 751 K, ou 477 °C, bem acima do ponto de ignição de muitos combustíveis. É por isso que um motor de alta compressão requer combustíveis especialmente formulados para não entrarem em autoignição (o que causaria o bater das bielas do motor quando operado sob estas condições de temperatura e pressão), ou que um supercompressor e intercooler que forneçam uma temperatura menor mantendo a mesma pressão. Um motor a diesel opera sob condições ainda mais extremas, com taxas de compressão de 20:1 ou mais, para fornecer uma alta temperatura de gás, que garanta a ignição imediata do combustível injetado.